题目链接:
算术表达式有前缀表示法、中缀表示法和后缀表示法等形式。
日常使用的算术表达式是採用中缀表示法,即二元运算符位于两个运算数中间。
请设计程序将中缀表达式转换为后缀表达式。
输入格式说明:
输入在一行中给出不含空格的中缀表达式,可包括+、-、*、\以及左右括号()。表达式不超过20个字符。
输出格式说明:
在一行中输出转换后的后缀表达式。要求不同对象(运算数、运算符号)之间以空格分隔。但结尾不得有多余空格。
例子输入与输出:
| 序号 | 输入 | 输出 |
| 1 | 2+3*(7-4)+8/4 | 2 3 7 4 - * + 8 4 / + |
| 2 | ((2+3)*4-(8+2))/5 | 2 3 + 4 * 8 2 + - 5 / |
| 3 | 1314+25.5*12 | 1314 25.5 12 * + |
| 4 | -2*(+3) | -2 3 * |
| 5 | 123 | 123 |
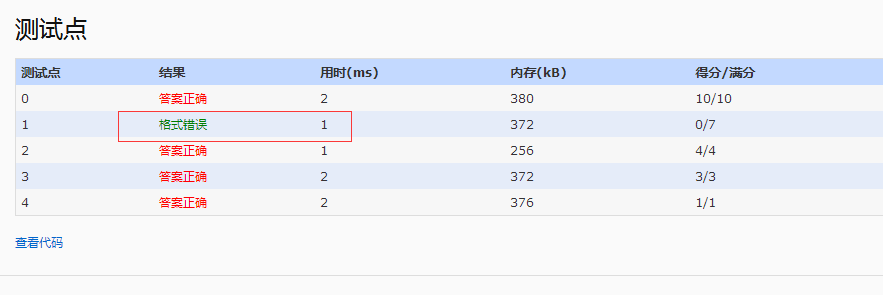
PS:起初第一天晚上做了好久。一直有个案例是PE。PE到吐也没过掉;
(甚至都有去找陈越姥姥求案例了的想法了)
终于没有去,第二天晚上又坐在电脑前想了各种案例,改了半天终于过掉了,
可是由于改动的地方太多。所以生成了如今这渣的不忍直视的代码,
此代码仅留作纪念(实在不忍直视)。
代码例如以下:
#include#include #include #include #include using namespace std;const int maxn = 520;stack ss;char s[maxn];int isnum(char c){ if((c>='0' && c<='9') || c=='.') return 1; return 0;}int val_op(char c){ if(c == '(' || c == ')') return 1; else if(c == '+' || c == '-') return 2; else if(c == '*' || c == '/') return 3; return 0;}int main(){ scanf("%s",s); int len = strlen(s); int flag = 0, mark = 0; int k = 0; for(int i = 0; i < len; i++) { if(i == 0) { if(s[i] == '(' && (s[i+1]=='+'||s[i+1]=='-')) { continue; } } if(i == 0)//为了防止相似:-2*(+3)的案例 { if(s[i]=='-' || s[i] == '+') { k++; printf("%c",s[0]); continue; } } //printf("size:%d",ss.size()); if(isnum(s[i]))//遇到运算数直接输出 { if(!flag) { flag = 1; k++; while(isnum(s[i])) { k++; printf("%c",s[i]); i++; } i--;//由于前面多加了一次 continue; //printf("%c",s[i]); } else if(mark == 0)//为了防止相似:-2*(+3)的案例 { k++; printf("%c",s[i]); } else { k++; printf(" %c",s[i]); mark = 0; } continue; } mark = 1;//为了防止相似:-2*(+3)的案例 if(s[i-1] == '(' && (s[i]=='+')) { if(flag || k!=0) printf(" "); while(isnum(s[++i])) { k++; printf("%c",s[i]); } i--;//由于前面多加了一次 continue; } else if(s[i-1] == '(' && s[i] == '-') { if(flag || k!=0) printf(" -"); else printf("-"); while(isnum(s[++i])) { k++; printf("%c",s[i]); } i--;//由于前面多加了一次 continue; } if(s[i] == '(')//遇到左括号压入栈 { ss.push(s[i]); } else if(s[i] == ')')//遇到右括号把栈内的运算符输出知道遇到左括号 { if(ss.size()==0) continue; while(ss.top()!='(') { k++; printf(" %c",ss.top()); ss.pop(); } // printf(" d%cd ",ss.top()); ss.pop(); } else if(ss.size()) { if(val_op(s[i]) <= val_op(ss.top()))//假设遇到的运算符的优先级小于等于栈顶运算符 { while(ss.size()) { char tc = ss.top(); if(val_op(tc) < val_op(s[i]))//直到当前运算符的优先级大于栈顶运算符 { //ss.push(tc); break; } if(tc!='(' && tc != ')') { k++; printf(" %c",tc); } ss.pop(); } } } if(s[i]!='(' && s[i]!=')') ss.push(s[i]); } if(ss.size())//输出栈内的运算符 { int len = ss.size(); for(int i = 0; i < len; i++) { if(ss.top()!='(' && ss.top()!=')') { k++; printf(" %c",ss.top()); } ss.pop(); } } printf("\n"); return 0;}/*2+3*(7-4)+8/4//2 3 7 4 - * + 8 4 / +((2+3)*4-(8+2))/5//2 3 + 4 * 8 2 + - 5 /1314+25.5*12//1314 25.5 12 * +2*(9+6/3-5)+4//2 9 6 3 / + 5 - * 4 +-2*(+3)//-2 3 *123//1231.2+(-5)+(+8)//1.2 -5 + 8 +-10.25+(-567)+(+563)//-10.25 -567 + 563 +(-656)//-656(-21)-(-4552)//-21 -4552 -(+21)-(-4564)//21 -4564 -(21)//21*/